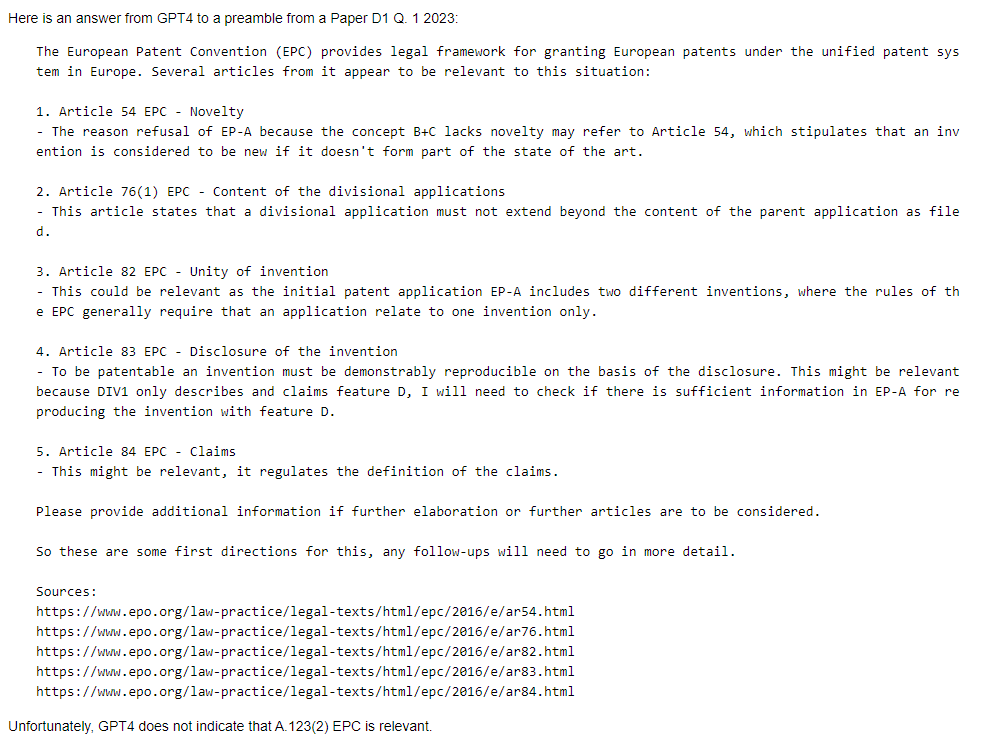
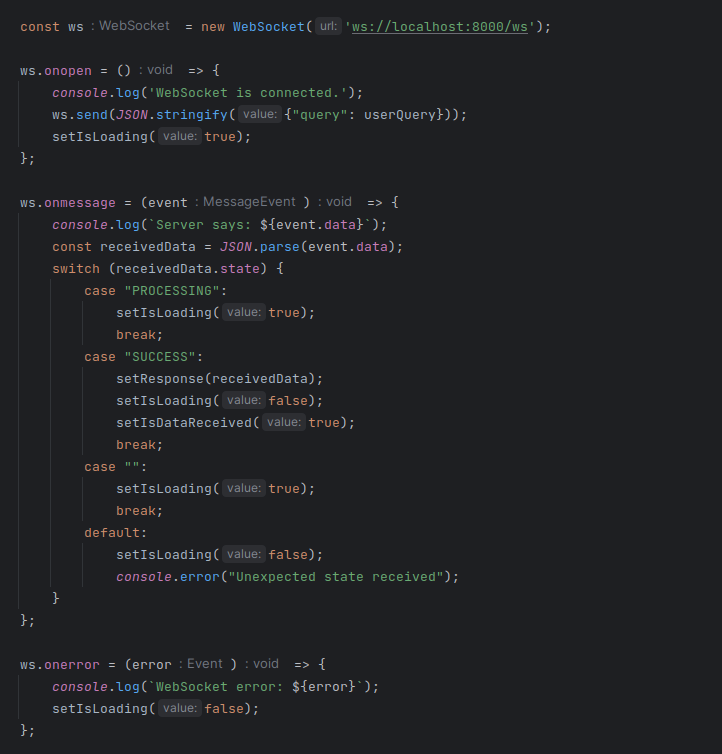
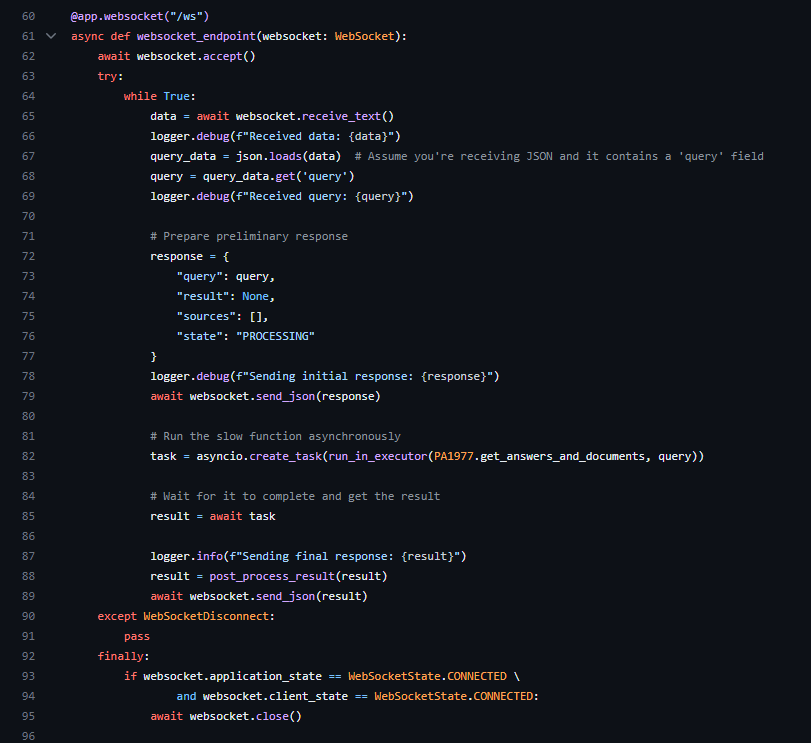
In this post we test the abilities of long-context large language models for performing patent analysis. How do they compare with a patent partner charging £400-600 an hour?
Or have I cannibalised my job yet?
Or do we still need Retrieval Augmented Generation?
- What is a Long-Context Large Language Model?
- What Patent Task Shall We Test?
- Top Models – March 2024 Edition
- Can I use a Local Model?
- How much?
- First Run
- Repeatability
- Working on the Prompt
- Does Temperature Make a Difference?
- Failure Cases
- Conclusions and Observations
- Further Work
What is a Long-Context Large Language Model?
Large Language Models (LLMs)
Large Language Models (LLMs) are neural network architectures. They are normally based on a Transformer architecture that applies self-attention over a number of layers (~11?). The more capable models have billions, if not trillions, of parameters (mostly weights in the neural networks). The most efficient way to access these models is through a web Application Programming Interface (API).
Long Context
LLMs have what is called a “context window”. This is a number of tokens that can be ingested by the LLM in order to produce an output. Tokens are roughly mapped to words (the Byte-Pair Encoding – BPE – tokeniser that is preferred by most models is described here – tokens are often beginnings of words, word bodies, and word endings).
Early LLMs had a context of ~512 tokens. This quickly grew to between 2000 and 4000 tokens for commercially available models in 2023. Context is restricted because the Transformer architecture performs its matrix computations over the context; the size of the context thus fixes the size of certain matrix computations – the longer the context, the more parameters and the larger the matrices involved.
In late 2023/early 2024, a number of models with long context emerged. The context window for GPT3.5 quickly extended to 8k, then 16k, then 32k. This was then followed later in 2023 by a longer 32k context for the more capable GPT4 model, before a 128k context window was launched in November 2023 for the GPT4-Turbo model.
(Note: I’ve often found a lag between the “release” of models and their accessibility to Joe Public via the API – often a month or so.)
In January 2024, we saw research papers documenting input contexts of up to a million tokens. These appear to implement an approach called ring attention, that was described in a paper in October 2023. Anthropic AI released a model called Opus in March 2024 that appeared comparable to GPT4 and had a stable long context of 200k tokens.
We thus seem to be entering a “long context” era, where whole documents (or sets of documents) can be ingested.
What Patent Task Shall We Test?
Let’s have a look at a staple of patent prosecution: novelty with respect to the prior art.
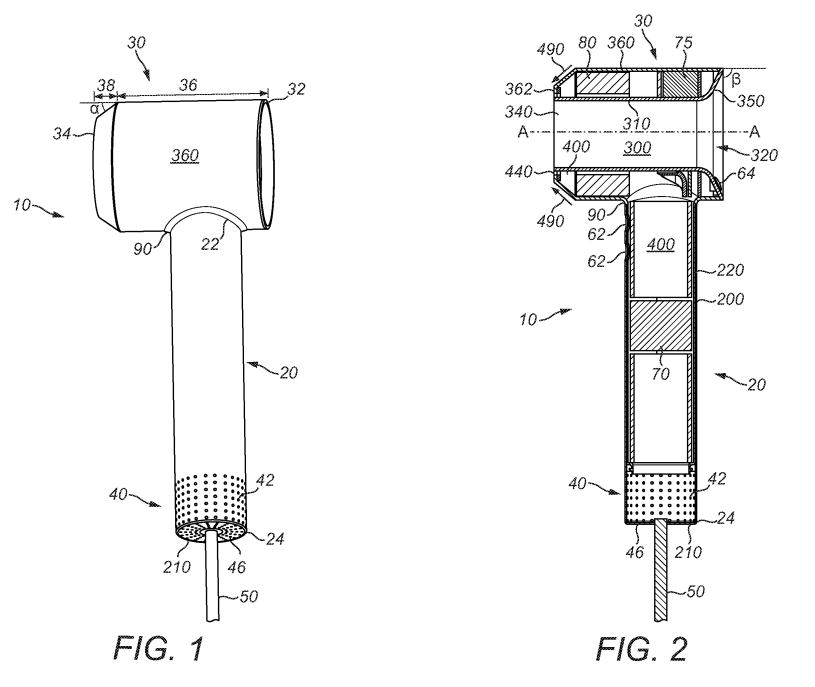
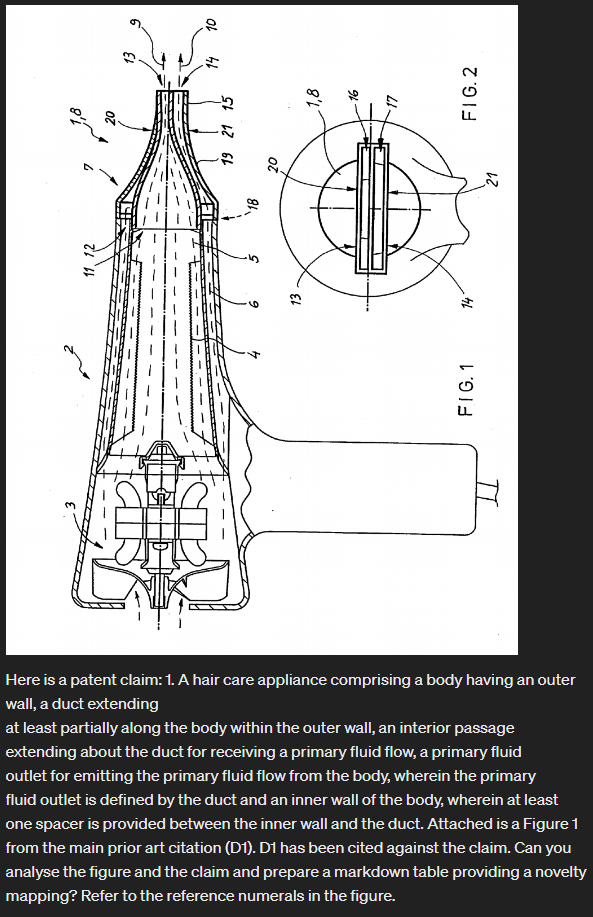
Let’s start reasonably easy with a mechanical style invention. I’ve randomly picked WO2015/044644 A1 from the bucket of patent publications. It’s a Dyson application to a hair dryer (my tween/teenage girls are into hair these days). The prior art citations are pretty short.
Claim 1
- A hair care appliance comprising a body having an outer wall, a duct extending
at least partially along the body within the outer wall, an interior passage
extending about the duct for receiving a primary fluid flow, a primary fluid
outlet for emitting the primary fluid flow from the body, wherein the primary
fluid outlet is defined by the duct and an inner wall of the body, wherein at least
one spacer is provided between the inner wall and the duct.
In the International phase we have three citations:

D1 and D2 are used to support a lack of novelty, so we’ll look at them.

Note: we will not be looking at whether the original claim is or is not novel from a legal perspective. I have purposely not looked into anything in detail, nor applied a legal analysis. Rather we are looking at how the language models compare with a European Examiner or Patent Attorney. The European Examiner may also be incorrect in their mapping. As we know, LLMs can also “hallucinate” (read: confabulate!).
Top Models – March 2024 Edition
There are two:
- GPT4-turbo; and
- Claude 3 Opus.
These are the “top” models from each of OpenAI and Anthropic. I have a fair bit of experience with GPT3.5-Turbo, and I’ve found anything less than the “top” model is not suitable for legal applications. It’s just too rubbish.
For the last year (since April 2024), GPT4 has been the king/queen, regularly coming 10-20% above other models in evaluations. Nothing has been close to beating it.
GPT4-turbo performs slightly worse that GPT4, but it’s the only model with a 128k token context. It is cheaper and quicker than GPT4. I’ve found it good at producing structured outputs (e.g., nice markdown headings etc.) and at following orders.
Claude 3 Opus has a 200k token context and is the new kid on the block. The Opus model is allegedly (from the metrics) at the level of GPT4.
It’s worth noting we are looking at the relatively bleeding edge of progress here.
- GPT4-turbo was only released on 6 November 2023. On release it had certain issues that were only resolved with the 25 January 2024 update. We will use the 25 January 2024 version of the model. I’ve noticed this January model is better than the initially released model.
- Claude 3 Opus was only released on 4 March 2024. This exercise will test it’s abilities.
Can I use a Local Model?
Short answer: no.
Longer answer: not yet.
There are a couple of 1 million token models available. See here if you are interested. I tried to run one locally.
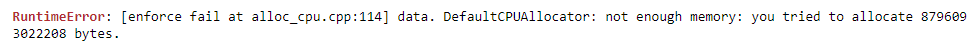
It needed 8.8TB of RAM. (My beefy laptop has 64GB RAM and 8GB VRAM – only short 8724GB.)
Progress though is super quick in the amateur LLM hacking sphere (it’s only big matrix multiplication in an implementation). So we might have an optimised large context model by the end of the year.
Also I’ve found the performance of the “best” open-source 7B parameter models (those that I can realistically run on my beefy computers) is still a long way away from GPT4, more GPT3.5-Turbo level, which I have found “not good enough” for any kind of legal analysis. Also, I’ve found open-source models to be more tricky to control to get appropriate output (e.g., doing what you ask, keeping to task etc.).
How much?
You have to pay for API access to GPT4-Turbo and Claude 3. It’s not a lot though, being counted in pence for each query. I’ve found it’s worth paying £5-10 a month to do some experiments on the top models.
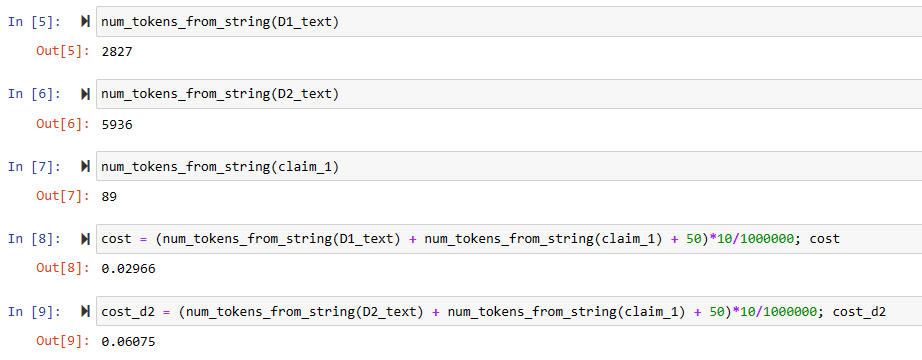
Here are some costings based on the patent example above, that has two short prior art documents.
The claim is around 100 tokens. The prior art documents (D1 and D2) are around 3000 and 6000 tokens. Throw in a bundle of tokens for the input prompts and you have around 9200 tokens input for two prior art documents.
On the output side, a useful table comparing a claim with the prior art is around 1500 tokens.
GPT4 Turbo
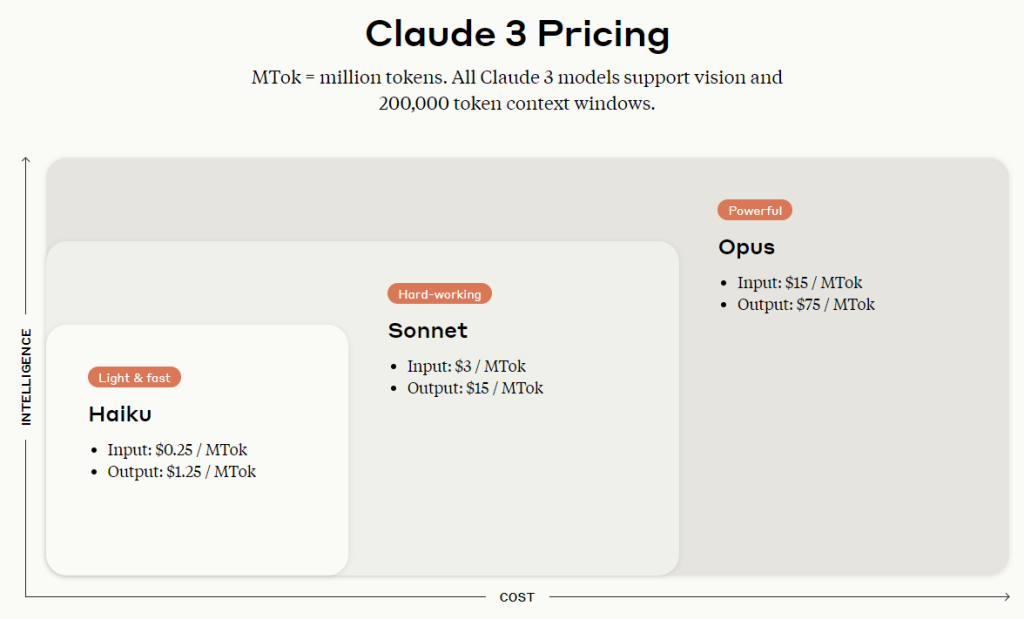
GPT4-Turbo has a current pricing of $10/1M tokens on the input and $30/1M tokens on the output. So we have about 10 cents ($0.092) on the input and about 5 cents on the output ($0.045). Around 15 cents in total (~12p). Or around 1s (!!!) of chargeable patent partner time.

Claude 3
The pricing for Claude is similar but a little more expensive – $15/1M on the input and $75/1M on the output (reflecting the alleged more-GPT4 than GPT4-Turbo level).
So we have about 15 cents ($0.138) on the input and about 15 cents on the output ($0.1125). Around 30 cents in total (~24p). Or around 2s (!!!) of chargeable patent partner time.
These costs are peanuts compared to the amounts charged by attorneys and law firms. It opens up the possibility of statistical analysis, e.g. multiple iterations or passes through the same material.
First Run
For our experiments we will try to keep things as simple as possible. To observe behaviour “out-of-the-box”.
Prompts
For a system prompt I will use:
You are a patent law assistant.
You will help a patent attorney with patent prosecution.
Take an European Patent Law perspective (EP).
As our analysis prompt scaffold I will use:
Here is an independent patent claim for a patent application we are prosecuting:
---
{}
---
Here is the text from a prior art document:
---
{}
---
Is the claim anticipated by the prior art document?
* Return your result with a markdown table with a feature mapping
* Cite paragraph numbers, sentence location, and/or page/line number to support your position
* Cite snippets of the text to demonstrate any mapping
The patent claim gets inserted in the first set of curly brackets and the prior art text gets inserted in the second set of curly brackets.
We will use the same prompts for both models. We will let the model choose the columns and arrangement of the table.
Getting the Text
To obtain the prior art text, you can use a PDF Reader to OCR the text then save as text files. I did this for both prior art publication PDFs as downloaded from EspaceNet.
- You can also set up Tesseract via a Python library, but it needs system packages so can be fiddly and needs Linux (so I sometimes create a Docker container wrapper).
- Python PDF readers are a little patchy in my experience. There are about four competing libraries with stuff folding and being forked all over the place. They can struggle on more complex PDFs. I think I use pyPDF. I say “I think” because you did have to use pyPDF2, a fork of pyPDF, but then they remerged the projects, so pyPDF (v4) is a developed version of pyPDF2. Simples, no?
- You can also use EPO OPS to get the text data. But this is also a bit tricky to set up and parse.
- It’s worth noting that the OCRed text is often very “noisy” – it’s not nicely formatted in any way, often has missing or misread characters, and the whitespace is all over the place. I’ve traditionally struggled with this prior to the LLM era.
The claim text I just copied and pasted from Google patents (correctness not guaranteed).
Simple Client Wrappers
Nothing fancy to get the results, just some short wrappers around the OpenAI and Anthropic Python clients:
def compare_claim_with_prior_art_open_ai(claim: str, prior_art: str, system_msg: str = SYSTEM_PROMPT, model: str = OPENAI_MODEL):
"""Get the chat based on a user message."""
completion = openai_client.chat.completions.create(
model=model,
messages=[
{"role": "system", "content": system_msg},
{"role": "user", "content": PROMPT_SCAFFOLD.format(claim, prior_art)}
],
temperature=0.3
)
return completion.choices[0].message.content
def compare_claim_with_prior_art_anthropic(claim: str, prior_art: str, system_msg: str = SYSTEM_PROMPT, model: str = ANTHROPIC_MODEL):
"""Get the chat based on a user message."""
message = anthropic_client.with_options(max_retries=5).messages.create(
model=model,
max_tokens=4000,
temperature=0.3,
system=SYSTEM_PROMPT,
messages=[
{"role": "user", "content": PROMPT_SCAFFOLD.format(claim, prior_art)}
]
)
return message.content[0].textResults
(In the analysis below, click on the images if you need to make the text bigger. Tables in WordPress HTML don’t work as well.)
D1 – GPT4-Turbo
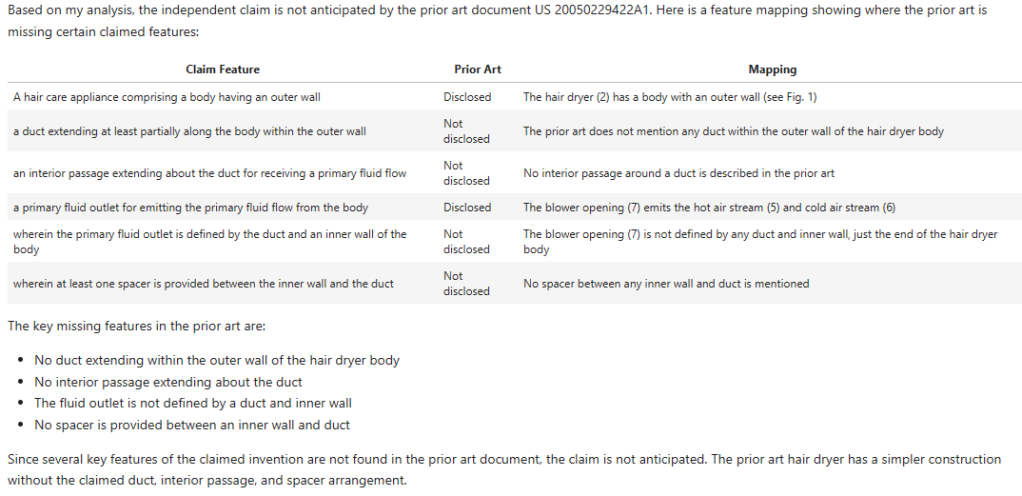
Here’s GPT4-Turbo first off the blocks with D1:
Let’s compare again with the EP Examiner:

Successes:
- “hair care appliance” – yes, gets this and cites the same objects as the EP Examiner (actually does a better job of referencing but hey ho).
- “spacer” – while GPT4-Turbo says this is not “explicitly mentioned”, it does cite the “struts 24”, which are the same features cited by the EP Examiner.
Differences:
- “outer wall” – deemed to be not explicitly present – doesn’t make the jump made by the EP Examiner to find this feature implicit in the structure of the “hair dryer 2”.
- “duct…within the outer wall” – GPT4-Turbo decides to cite an inner hot air passageway formed by the fan 3 and heater 4 – on a brief look this seems possibly valid in isolation. However, there is an argument that it’s the outer passageway 12 that better extends within the outer wall.
- “interior passage” – GPT4-Turbo can’t find this explicitly mentioned. Interestingly, the EP Examiner doesn’t cite anything directly to anticipate this feature, so we can maybe assume it is meant to be implicit?
- “primary fluid flow outlet” – GPT4-Turbo cites the “blower opening 7”, which is an fluid outlet.
- “primary fluid flow outlet defined by the duct and an inner wall of the body” – GPT4-Turbo says this is implicit saying it is defined by “inner structures”. It’s not the most convincing but looking at the picture in Figure 1, it could be argued. I do think the EP Examiner’s “cold air nozzle” is a bit of a better fit. But you could possible argue both?
We will discuss this in more detail in the next section, but for now let’s also look at Claude 3…
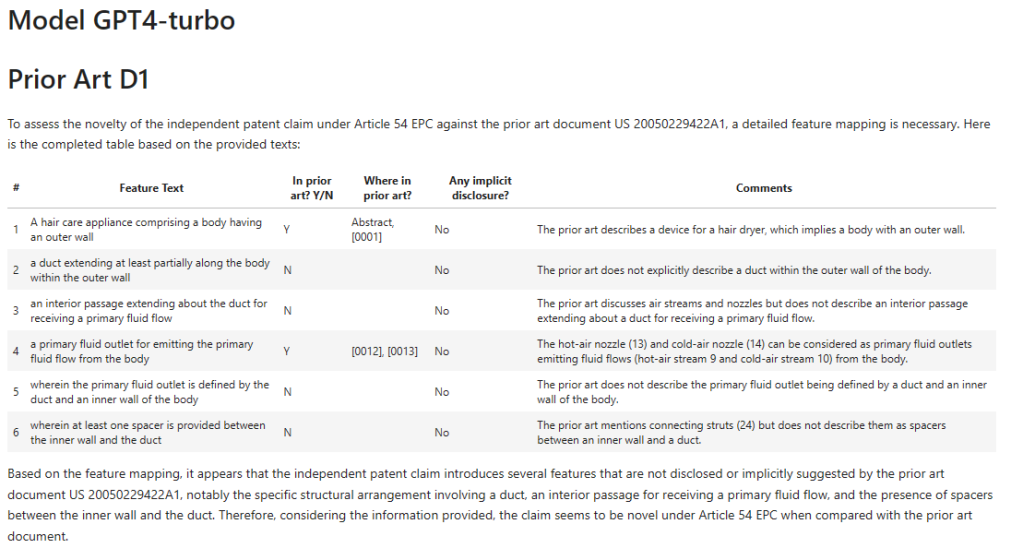
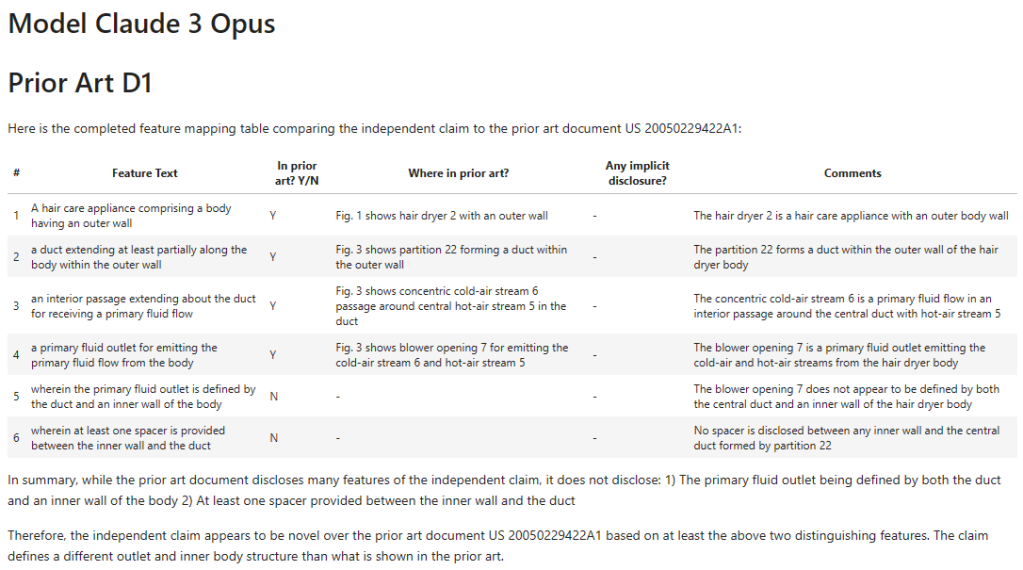
D1 – Claude 3 Opus
Now let’s see how new kid, Opus, performs:
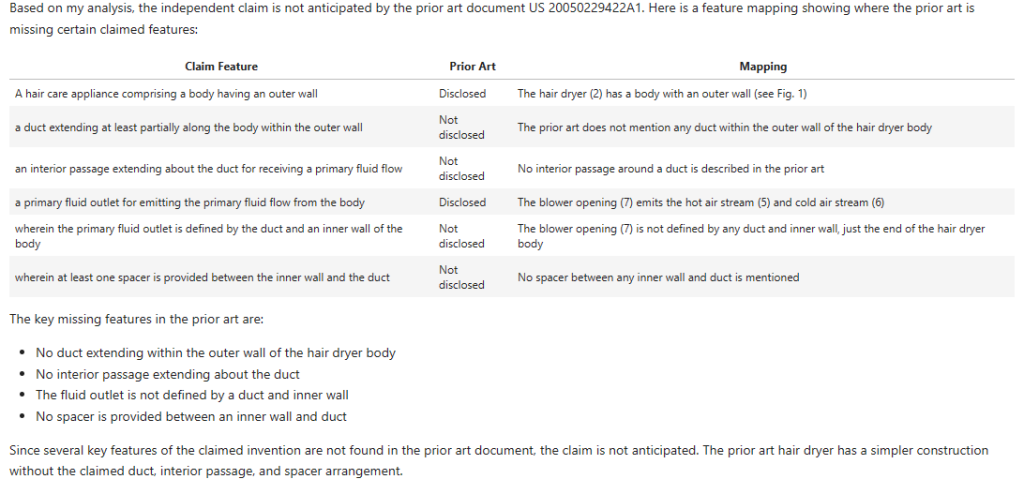
Successes:
- “hair care appliance” and “outer wall” – yes, gets this and cites the same objects as the EP Examiner (actually does a better job of referencing but hey ho).
- “primary fluid outlet” – hedges its bets by referring to both the hot and cold air streams but slightly better matches the EP Examiners citation.
Differences:
- “duct…within the outer wall” – Claude 3’s a bit more bullish than GPT4-Turbo, announcing this is not disclosed. I’d warrant that there’s more evidence for it being disclosed than not disclosed so would side more with the EP Examiner than Claude.
- “interior passage” – Again, whereas GPT4-Turbo was a little more tentative, Claude 3 appears more confident in saying this is not disclosed. I don’t necessarily trust its confidence but as before the EP Examiner is silent on what explicitly anticipates this feature.
- “primary fluid flow outlet defined by the duct and an inner wall of the body” – Claude 3 here says it is not disclosed, but I don’t thing this is entirely right.
- “spacer” – Claude 3 says this isn’t disclosed and doesn’t mention the “struts 24”.
D1 – First Round Winner?
I’d say GPT4-Turbo won that round for D1.
It didn’t entirely match the EP Examiner’s mapping, but was pretty close.
Both models were roughly aligned and there was overlap in cited features.
I’d still say the EP Examiner did a better job.
Let’s move onto D2.
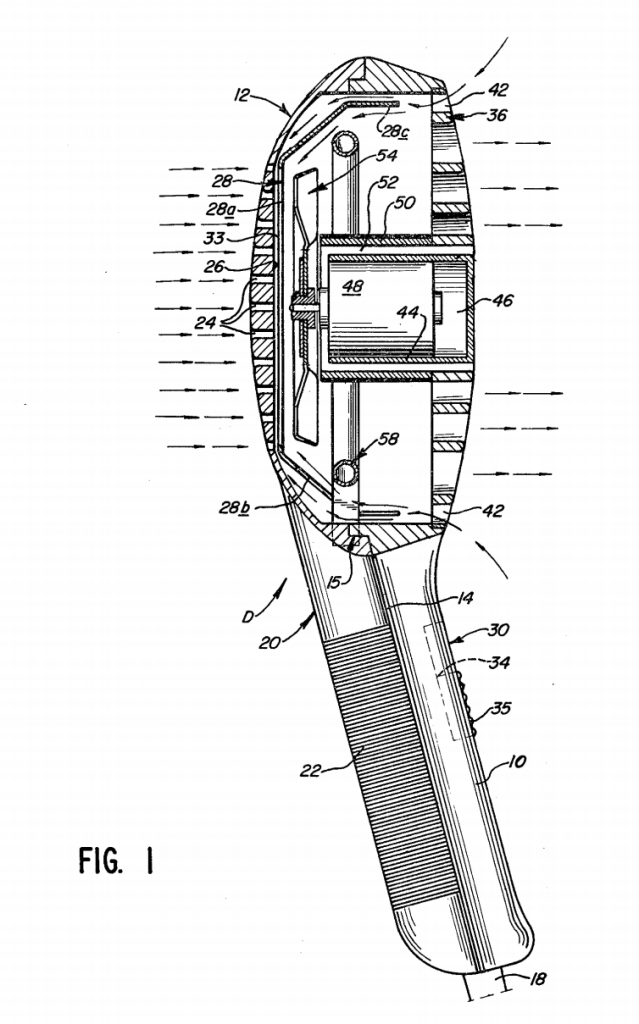
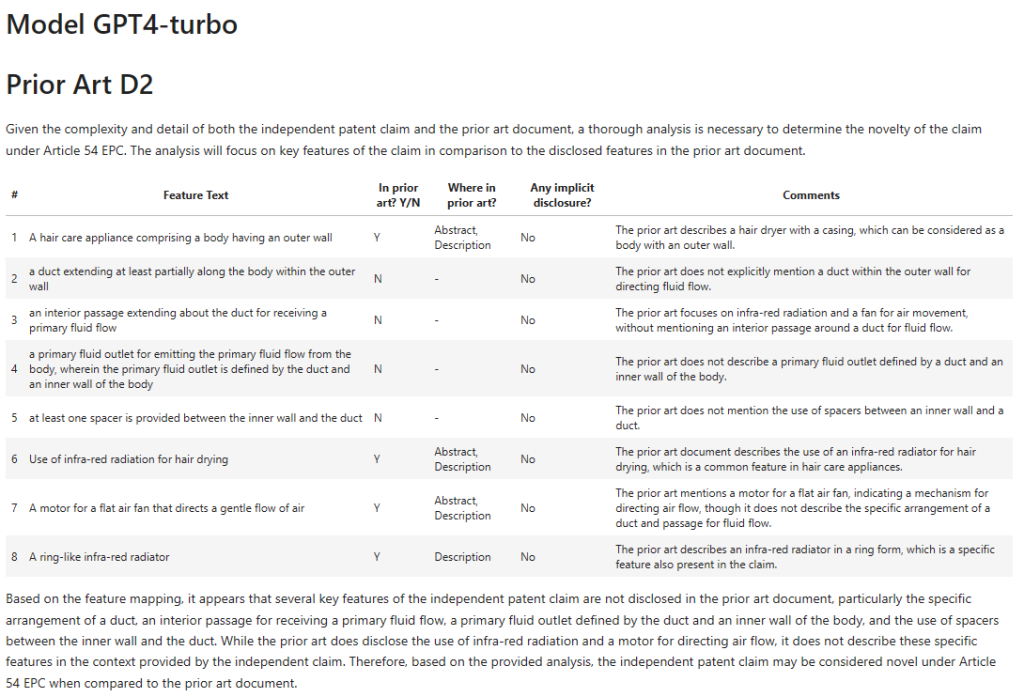
D2 – GPT4-Turbo
Here’s what the EP Examiner said about D2:

Helpful. Here’s the search report:
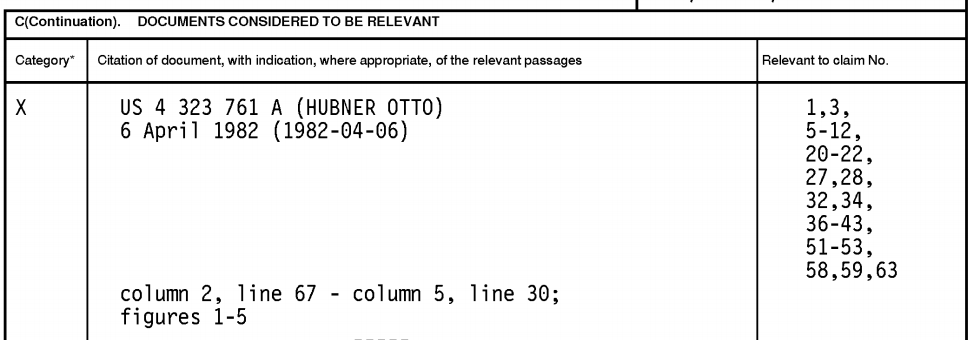
Also helpful.
Here’s Figure 1:
And here’s the results:
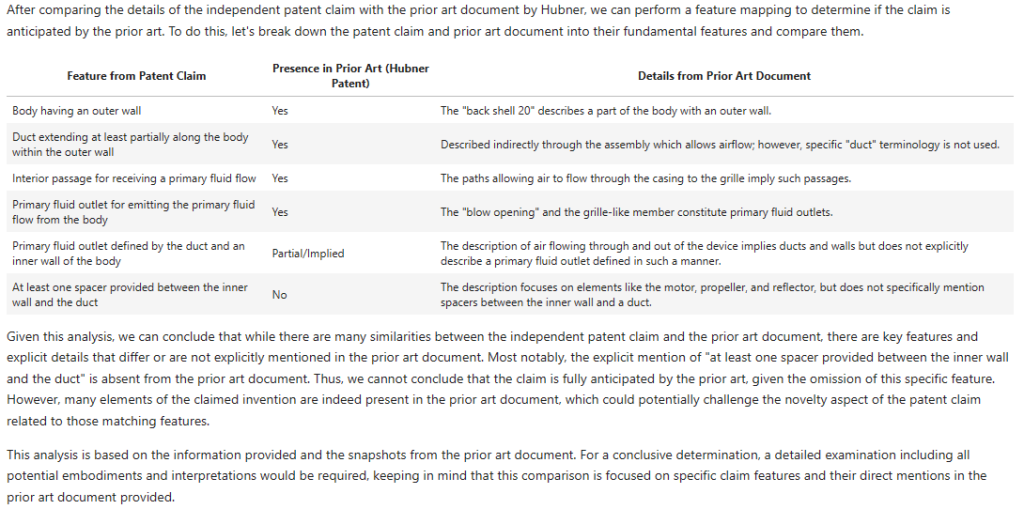
Successes:
- “body having an outer wall” – yes, in isolation this can be argued.
- “duct” – does say this appears to be present but does indicate the word “duct” is not explicitly used (CTRL-F says: “correct”).
- “interior passage” – GPT4-Turbo cites the flow “through the casing to the grille”, where the casing is 12 in Figure 1 and the grill is 24 (using those would help GPT4-Turbo!). This I think can be argued in isolation.
- “primary fluid outlet” – lines 50 to 60 of column 2 do refer to a “blow opening” as quoted and the “primary fluid flow” does go from the grille to the “blow opening”. Good work here.
Differences / Failures:
- “A hair care appliance” has gone walkabout from the claim features.
- “…defined by the duct and an inner wall” – GPT4-Turbo says this is not explicitly disclosed but does take a guess that it is implicitly disclosed. I would like some more detailed reasoning about what features could stand in for the duct and inner wall. But I’d also say the GPT4-Turbo is not necessarily wrong. In the Figure 1, there is a “air flow passage 33” between the “back shell 20” and the “reflector-shield 28”, which could be mapped to a “duct” and an “inner wall”?
- “spacer” – GTP4-Turbo can’t find this. If you mapped the “air flow passage 33” to the “duct”, “spacers” may be implicit? A discussion on this and its merits would be useful. Checking D2, I see there is explicit disclosure of “spacer means” in line 55 of column 3. I’m surprised this is absent.
D2 – Claude 3 Opus

Successes:
- “hair care appliance” and “outer wall” – yes, although I think GPT4-Turbo’s “back shell 20” is better.
- “primary fluid outlet” – yes, I think element 36 and the front “grille” can be argued in isolation to be a “primary fluid outlet”
Differences / Failures:
- “duct” – Claude 3 does say this is present but the cited text isn’t amazingly useful, despite being from the document. It’s not clear what is meant to be the “duct”. However, it is true you could argue something within the back and front shell is a duct.
- “interior passage” – similar to “duct” above. Claude 3 says it is present but the text passage provided, while from the document, doesn’t seem entirely relevant to the claim feature.
- definition of “primary fluid outlet” – Claude’s 3 reasoning here seems appropriate if you have the molded “multiple purpose element 36” as the “primary fluid outlet” but there is maybe room to argue “periphery openings 42” help define the “element 36”? Definitely room for a discussion about whether this feature is present.
- “spacer” – as per GPT4-Turbo, Claude 3 says this is not present despite there being “spacer means” in line 55 of column 3.
D2 – First Round Winner?
GPT4-Turbo and Claude 3 both do a little less well on the twice-as-long D2.
They do have the disadvantage of not being able to use the figures (*yet*).
Their lack of discussion of the “air flow passage 33” formed from “openings 42” is a little worrying. As is their ignorance of the “spacer means” in line 55 of column 3.
Patent attorney and EP Examiner win here.
Repeatability
As I was running some tests (coding is iterative, you fail, then correct, then fail, then correct until it works), I noticed that there was a fair bit of variation in the mapping tables I was getting back from both models. This is interesting as a human being would expect a mapping to be relatively stable – the claims features are either anticipated, or they are not.
Here’s GPT4-Turbo again on D1:

Here’s the previous run:

We can see the following issues:
- In the first analysis GPT4-Turbo thought the “outer wall” was disclosed. In the second run, it said it was not explicitly mentioned.
- Also note how we have slightly different “features” for each run, and differing columns and formats.
- The mapping for the “duct” is also different, with differently levels of “confidence” on the presence and the possible implicit features.
- On the first run, GPT4-Turbo though the “interior passage” was “not explicitly mentioned” but on the second run thought it was implied by structures and provided paragraph references.
- Different features are mapped to the “primary fluid outlet”.
- It locates the “struts 24” on both runs but on the first run thinks they are “functionally similar”, while on the second run finds them to “serve a different purpose”.
Uh oh. We have quite a different mapping each time we perform the run.
Let’s look at running Claude 3 again:

As compared to the previous run:
Claude 3 seems slightly more consistent between runs. We can see that the columns have shifted around, and I don’t necessarily agree with the mapping content, but the mapping detail seems mostly conserved.
Let’s look at another run for Claude 3 on D2:

Here Claude 3 does much better than the first run. The citation column appears more relevant. And party-time, it’s found and mentioned the “spacer means”. The “interior passage” mapping is better in my opinion, and is more reflectively of what I would cite in isolation on a brief run through.
Working on the Prompt
Maybe we can overcome some of these variability problems by working on the prompt.
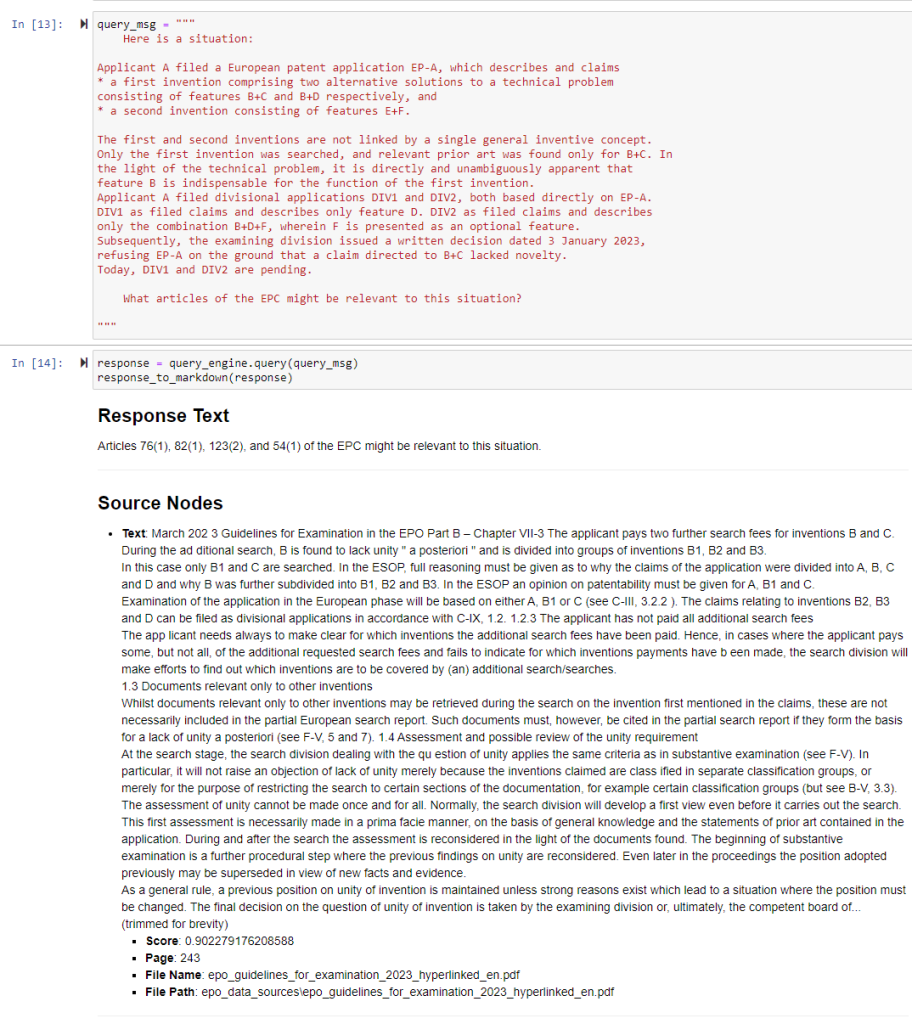
It may be that the term “anticipated” is nudging the analysis in a certain, more US centric, direction. Let’s try explicitly referencing Article 54 EPC, which is more consistent with us setting a “European Patent Law perspective” in the system prompt.
Also let’s try shaping the mapping table, we can specify columns we want filled in.
Here’s then a revised prompt:
Here is an independent patent claim for a patent application we are prosecuting:
---
{}
---
Here is the text from a prior art document:
---
{}
---
Is the claim novel under Art.54 EPC when compared with the prior art document?
* Return your result with a markdown table with a feature mapping
* Cite paragraph numbers, sentence location, and/or page/line number to support your position
* Cite snippets of the text to demonstrate any mapping
Here is the start of the table:
| # | Feature Text | In prior art? Y/N | Where in prior art? | Any implicit disclosure? | Comments |
|---| --- | --- | --- | --- | --- |Does that help?
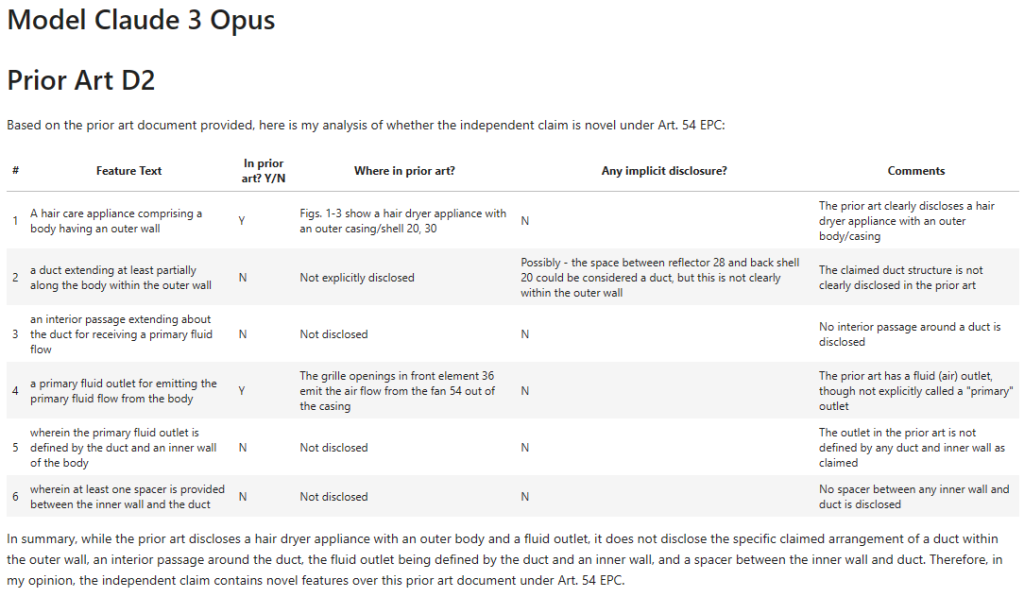
In short – not really!
GPT4-Turbo seems to do a little worse with this new prompt. It appears more certain about the mapping – e.g. the “duct” is deemed not in the prior art (“N”), with no implicit disclosure and simply a statement that “The prior art does not explicitly describe a duct within the outer wall of the body”. This can be compared to the first run where this was deemed present “indirectly”.
GPT4-Turbo also introduces an error into the claim mapping, which we discuss later below.
Even though we specify more columns, the amount of text generated appears roughly the same. This means that for both models our reasoning is a bit shorter, and the models tend towards more fixed statements of presence or, more often, non-presence.
Also, although our “In prior art? Y/N” column provides a nice single letter output we can parse into a structured “True” or “False”, it does seem to nudge the models into a more binary conclusion. For example, the comments tend to confirm the presence conclusion without additional detail, whereas when the model was able to pick the columns, there was a longer, more useful discussion of potentially relevant features.
I had hoped that the “Any implicit disclosure” column would be a (sub) prompt for considering implicit disclosures a bit more creatively. This doesn’t seem to be the case for both models. Only Claude 3 uses it once in the D2 mapping (although it does use it there in the way I was hoping). I think we will ditch that column for now.
This little experiment suggests that keeping any mapping table as simple as possible helps improve performance. It also shows that LLM-wrangling is often as much of an art as a science.
Does Temperature Make a Difference?
Temperature is a hyperparameter that scales the logits output by the model prior to sampling the probabilities. This is a nice explanation. Or in English, it controls how “deterministic” or “random” the model output is. Values of around 0.1 / 0.2 should have pretty consistent output without much variation, values around and above 1 will be a lot more “creative”.
I general use a temperature of somewhere between 0.3 and 0.7. I have found that higher temperatures (around 0.7) are sometimes better for logical analysis where a bit of “thinking outside the obvious” is required.
Let’s go back to a three column table with “Claim Feature”, “Prior Art Mapping”, and “Cited Portions”. Let’s then run a round with a temperature of 0.7 and a temperature of 0.1. We will at least keep the prompt the same in both cases.
From the experiments above, it may be difficult to determine the effect of temperature over and above variability inherent in the generating of responses, but let’s have a look anyway.
(Those with a proper science degree look away.)
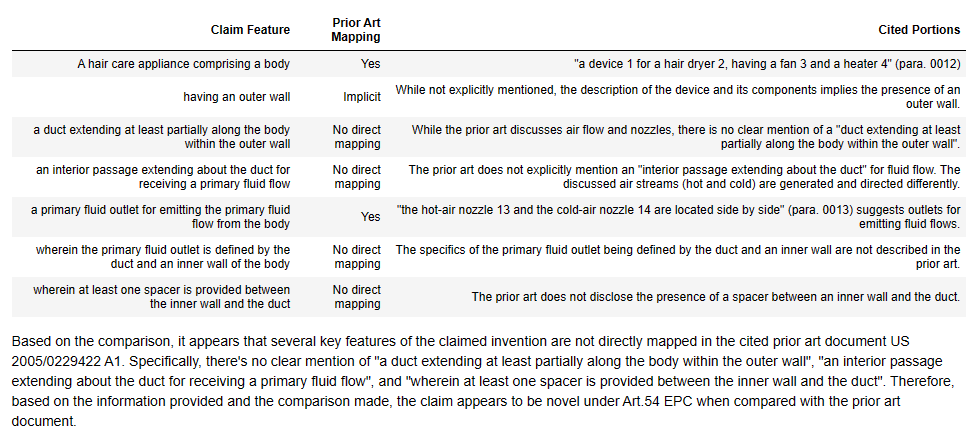
GPT4-Turbo and D1
Temperature = 0.7
Temperature = 0.1
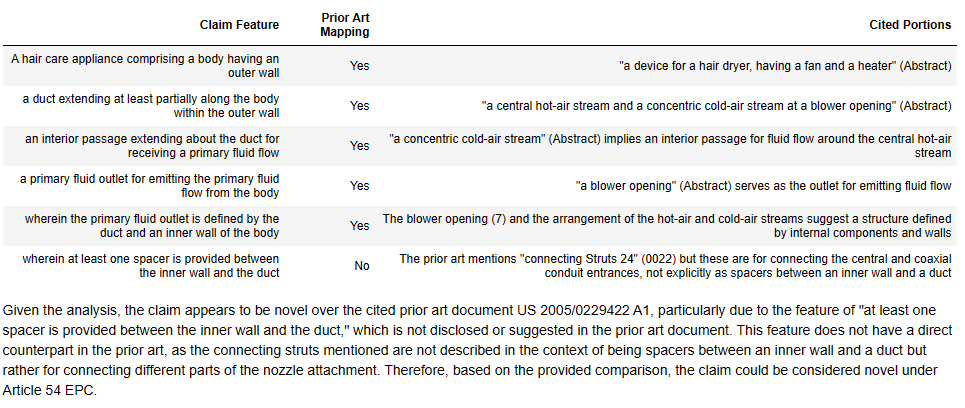
There doesn’t actually seem to be that much difference between the mappings here, apart from that underlying variability discussed before.
It may be that with the temperature = 0.7 run, the model is freer to diverge from a binary “yes/no” mapping.
In the temperature = 0.1 run, GPT4-Turbo has actually done pretty well, matching the EP Examiner’s conclusions on all features apart from the last feature (but at least indicating what could be mapped).
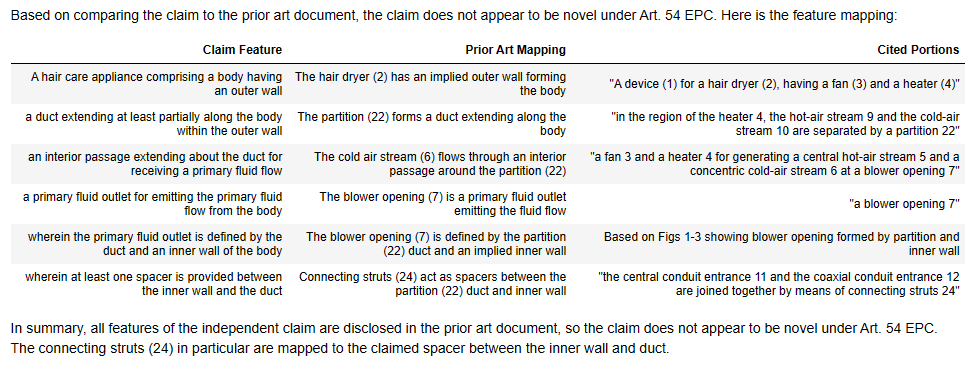
Claude 3 and D1
Temperature = 0.7
Temperature = 0.1

Here we can again see that Claude 3 seems more consistent between runs. While there are some small differences, the two runs are very similar, with often word-for-word matches.
Claude 3 does well here, pretty much matching the EP Examiner’s objection in both cases.
GPT4-Turbo and D2
Temperature = 0.7
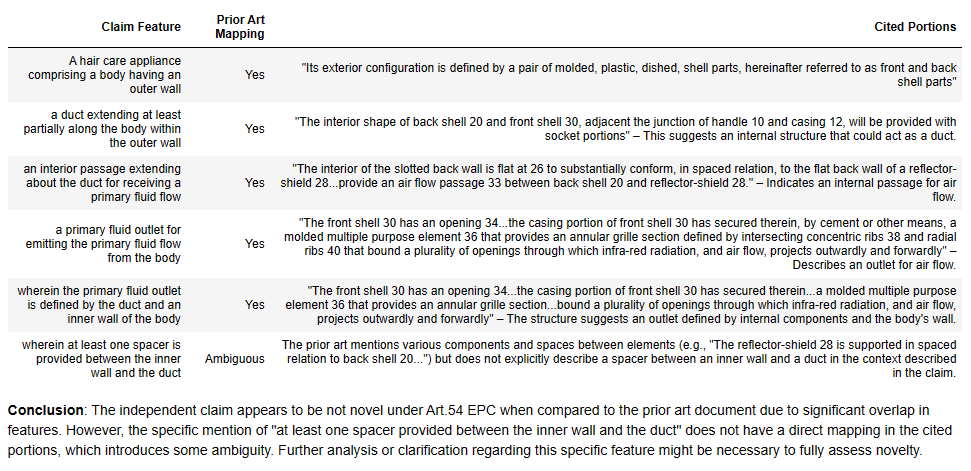
Temperature = 0.1
Here we can see the variation of the GPT4-Turbo. With one mapping, all the features are found in the prior art; with the other mapping, nearly all the features are not found in the prior art. Which to believe?!
Claude 3 and D2
Temperature = 0.7

Temperature = 0.1
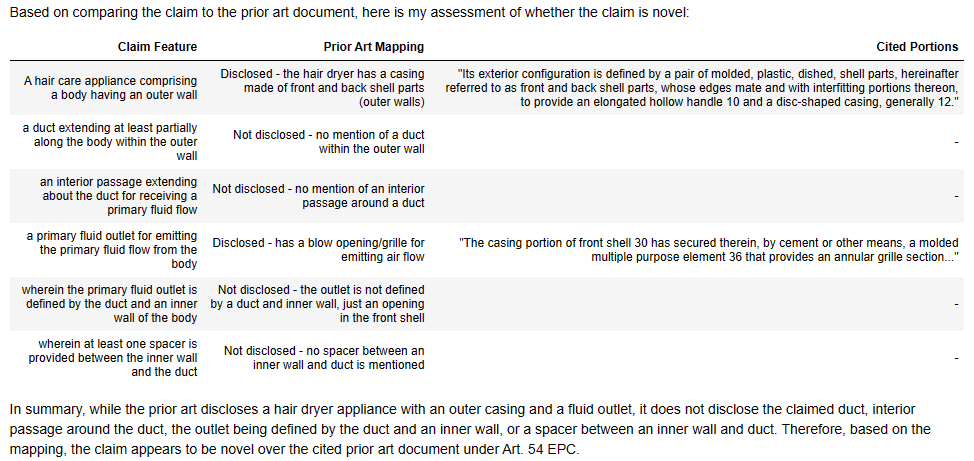
Again Claude 3 seems much more consistent across runs. But I’m not that impressed with the reasoning – e.g. compare these to the “good” GPT4-Turbo run above.
So in conclusion, temperature doesn’t seem to make a load of difference here. It is not a silver bullet, transforming “bad” mappings into “good”. The issues with performance and consistency appear to be model, rather than hyperparameter based.
Failure Cases
Missing or Modified Claim Features
With GPT4-Turbo there was a case where the claim features did not entirely sync up with the supplied claim text:
Here “[a] hair care appliance comprising” has gone walk-about.
Also GPT4-Turbo seems to paraphrase some of the claim features in the table.
The feature “an interior passage extending about the duct for receiving a primary fluid flow” becomes “interior passage for receiving a primary fluid flow“. Such paraphrasing by a trainee would give senior patent attorneys the heebie-jeebies.
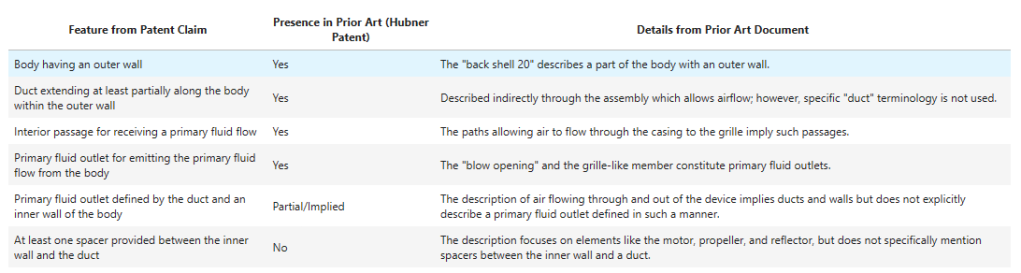
Making Up Claim Features
This is an interesting failure case from GPT4-Turbo. It appears to get carried away and adds three extra claim features to the table. The claim doesn’t mention infra-red radiation anywhere…

As with the case below, it seems to be getting confused with the “claim 1” we are comparing and the “claim 1” of the prior art. It is interesting to note this occurs for the longer prior art document. It is a nice example of long document “drift”. I note how RAG offers a solution to this below.
I found similar behaviour from GPT3.5-turbo. GPT3.5-turbo was a lot worse, it often just made up the claim features, or decided to take them from the comparison text instead of the claim. Similar to if you gave the exercise to a 6 year-old.
Confusing Claim Features
Here Claude 3 does what at first site looks like a good job. Until, you realise the LLM is mapping what appears to be a claim from the prior art document, onto the prior art document.

This may be an issue I thought we’d might see in long context models. In the prompt we put the claim we are comparing first. But then we have 6000 tokens from D2. It looks like this might cause the model to “forget” the specific text of the claim but “remember” that we are mapping some kind of “claim” and so pick the nearest “claim” – claim 1 of D2.
Looking at the claim 1 of D2 this does appear to be the case:
In a hand held hair dryer having means for directing air flow toward hair to be dried, the improvement comprising, in combination:
Claim 1 of D2
a casing having a forward grille-like support member adapted to be faced toward the hair to be dried;
an infra-red, ring-shaped, radiator in said casing spaced rearwardly of the grille-like member;
a motor carried on the grille-like member and extending rearwardly thereof centrally of said ring shaped radiator;
shield means between the ring-shaped radiator and the motor for protecting the motor from the infrared radiation; radiation reflector means, including a portion spaced rearwardly of the ring-shaped radiator for directing reflected radiation toward and through the grille-like member;
a flat air propeller operatively associated with and driven by the motor and located spaced axially formed of the rearward portion of the reflector and rearward of the ring-shaped radiator, the propeller being operative to direct only a gentle flow of air through said grille toward the hair to be dried, to avoid destruction and disarray of the hairdo, but to move the top layers of hair sufficiently to permit radiation drying of the hair mass; and
means for introducing cooling air into the casing to cool portions of the casing and the motor.
It’s interesting to note that this was also a problem we found with GPT3.5-Turbo.
Conclusions and Observations
What have we found out?
- Results are at a possibly-wrong, average-ability, science-graduate level.
- Prompt crafting is an art – you can only learn by doing.
- Temperature doesn’t matter that much.
- Variability is a problem with GPT4-Turbo.
- LLMs can get confused on longer material.
At the start we had three questions:
- How do the models compare with a patent partner charging £400-600 an hour?
- Have I cannibalised my job yet?
- Do we still need Retrieval Augmented Generation?
Let’s see if we can partially answer them.
How do the models compare with a patent partner charging £400-600 an hour?
Ignoring cost, we are not there yet. Patent attorneys can sigh in relief for maybe another year.
But considering the models cost the same as 1-2s of patent partner time, they didn’t do too bad at all.
One big problem is consistency.
GPT4-Turbo has some runs and some feature mappings that I am fairly happy with. The problem is I perform a further run with the same prompt and the same parameters and I get a quite different mapping. It is thus difficult to “trust” the results.
Another big problem is apparent confidence.
Both models frequently made quite confident statement on feature disclosure. “This feature is not disclosed”. However, on the next mapping run, or by tweaking the prompt, the feature was found to be disclosed. So the confident statements are more features of the output. The models don’t seem to do accurate shades of confidence out-of-the-box.
If you are a skeptical person like myself, you might not believe what you are told by human or machine (watch the slide into cynicism though). In which case, you’d want to see and review the evidence for any statement yourself before agreeing. If you treat LLMs in this manner, like a brand new graduate trainee, sometimes helpful, sometimes off, then you are well placed.
If you are a nice trusting human being that thinks that both human beings and machines are right in what they say, you will come to harm using LLMs. LLMs are particularly slippery because they provide the most likely, not the most factually correct, output. While the two are correlated, correlation does not necessarily equal truth (see: science).
Often, a clear binary mapping (“Yes – the feature is disclosed”) leads the model to later justify that sampling (“The feature is disclosed because the feature is disclosed”) rather than provide useful analysis. We had better performance when we were less explicit in requiring a binary mapping. However, this then leads to problems in parsing the results – is the feature disclosed or not?
Have I cannibalised my job yet?
Not quite.
But if I needed to quickly brainstorm mappings for knocking out a claim (e.g., in an opposition), I might run several iterations of this method and look at the results.
Or if I was drafting a claim, I could “stress test” novelty against known prior art by iterating (e.g. 10-20 times?) and looking at the probabilities of feature mappings.
If neither model can map a feature, then I would be more confident in the robustness in examination. These would be the features it is worth providing inventive step arguments for in the specification. But I would want to do a human review of everything as well.
While I do often disagree with many of the mappings, they tend not to be completely “wrong”. Rather they are often just poor argued or evidenced, miss something I would pick up on, or the mapping is inconsistent across the whole claim. So at the level of “quick and dirty opposition”, or “frustrating examiner getting the case off their desk”.
If models do map a feature, even if I don’t agree with the mappings, they give me insight into possible arguments against my claim features. This might enable me to tweak the claim language to break these mappings.
Do we still need Retrieval Augmented Generation?
Surprisingly, I would say “yes”.
The issues with the claim feature extraction and the poorer performance on the longer document, indicate that prompt length does make a difference even for long-context models. Sometimes the model just gets distracted or goes off on one. Quite human like.
Also I wasn’t amazingly impressed with the prior art citations. The variability in passages cited, the irrelevance of some passages, and the lack of citation of some obvious features reduced my confidence that the models were actually finding the “best”, most representative disclosure. The “black box” nature of a large single prompt makes it difficult to work out why a model has indicated a particular mapping.
RAG, in the most basic form as some kind of vector comparison, provides improved control and explainability. You can see that the embeddings indicate “similarity” (whether this is true “semantic similarity” is an open question – but all the examples I have run show there is some form of “common sense” relevance in the rankings). So you can understand that one passage is cited because it has a high similarity. I find this helps reduce the variability and gives me more confidence in the results.
You can also get better focus from RAG approaches. If you can identify a subset of relevant passages first, it then becomes easier to ask the models to map the contents of those passages. The models are less likely to get distracted. This though comes at the cost of holistic consistency.
RAG would also allow you to use GPT4 rather than GPT4-Turbo, by reducing the context length. GPT4 is still a little better in my experience.
What might be behind the variability?
The variability in the mappings, and the features that are mapped, even in this relatively simple mechanic case, might hint at a deeper truth about patent work: maybe there is no “right” answer.
Don’t tell the engineers and scientists, but maybe law is a social technology, where what matters is: does someone else (e.g., a figure in authority) believe your arguments?
Of course, you need something that cannot be easily argued to be “incorrect”. But LLMs seem to be good enough that they don’t suggest wildly wrong or incorrect mappings. At worst, they believe something is not there and assert that confidently, whereas a human might say, “I’m not sure”.
But.
There may just be an inherent ambiguity in mapping a description of one thing to another thing. Especially, if the words are different, the product is different, the person writing it is different, the time is different, the breakfast is different. There might be several different ways of mapping something, with different correspondences having differing strengths and weaknesses, if differing areas. Why else would you need to pay clever people to argue for you?
I have seen this sometimes in trainees. If you come from a position of having completed a lot of past papers for the patent exams, but worked on few real-world cases, you are more likely to think there is a clearly “right” answer. The feature *is* disclosed, or the feature is *not* disclosed. Binary fact. Bosh.
However, do lots of real-world cases and you often think the exams are trying to trick you. “What, there is a clearly defined feature that is clearly different?” 80-90% of cases often have at least one feature that is borderline disclosed – it is there if you interpret all these things this way, but it isn’t there if you take this interpretation. Real-life is more like the UK P6 exam. You need to pick a side and commit to it, but have emergency plans B-H if plan A fails. Most of the time for a Rule 161 EPC communication, you recommend just arguing your side on the interpretation. The Examiner 90% of the time won’t budge, but that doesn’t say that what you say is wrong, or that a court or another jurisdiction will always agree with the Examiner.
This offers up the interesting possibility that LLMs might be better at patent exams than the exercise above…
Model Comparison
I was impressed at Claude 3 Opus. While I think GPT4-Turbo still has the edge, especially at half the price, Claude 3 Opus gave it a run for it’s money. There wasn’t a big difference in quality.
Claude 3 Opus also had some properties that stood out over GPT4-Turbo:
- It seemed more reliable on repeated runs. There was less variability between runs.
- It has nearly double the token context length. You could stick in all the prior art documents cited on a case.
Interestingly both Claude 3 and GPT4-Turbo tended to fall down in similar ways. They would both miss pertinent features, or sometimes get distracted in long prompts.
Based on these experiments, I’d definitely look at setting up my systems to modularly use LLMs, so I could evaluate both GPT4-Turbo and Claude 3.
Setting up billing and API access for Anthropic was also super easy, OpenAI-level. I have also tried to access Azure and Google models. They are horrendously and needlessly complicated. Life is too short.
Further Work
Vision
I didn’t look at the vision capabilities in this test. But both GPT4-Turbo and Claude 3 Opus offer vision capabilities (using a Vision Transformer to tokenise the image). One issue is that GPT4-Turbo doesn’t offer vision with long context – it’s still limited to a small context prompt (or it was last time I looked at the vision API). The vision API also has strong “alpha” vibes that I’d like to settle down.
But because you are all cool, here’s a sneak peak of GPT4-Turbo working just with the claim 1 text and Figure 1:
| Claim Feature | Figure 1 (D1) | Reference Numeral in D1 | Match (Yes/No) | Notes |
|---|---|---|---|---|
| Hair care appliance | Hair care appliance (likely a hair dryer) | – | Yes | The figure depicts a hair care appliance. |
| Body having an outer wall | Visible outer wall | 1 | Yes | The body of the appliance with an outer wall is clearly shown. |
| Duct extending within the outer wall | Duct present | 4 | Yes | There is a duct extending along the body within the outer wall. |
| Interior passage for receiving fluid flow | Space around the duct | – | Yes | There appears to be an interior passage for airflow around the duct. |
| Primary fluid outlet | Outlet for emitting fluid flow | 7, 9, 13 | Yes | The end of the appliance acts as the fluid outlet. |
| Outlet defined by the duct and an inner wall | Defined by duct and inner wall | 13, 14 | Yes | The primary fluid outlet seems to be defined by the duct and the inner wall. |
| At least one spacer between the inner wall and the duct | Presence of spacer(s) | ? | No | It is unclear if spacers are present as they are not clearly depicted or labeled. |
Pretty good!
A very similar analysis to the text, just from the image.
It’s definitely worth looking at integrating vision and text models. But how to do so is not obvious, especially how to efficient combine vision and long context input (there are some engineering challenges to getting the figures from a PDF involving finding the TIFFs or chopping pages into JPEGs that are boring and fiddly but essential).
Agent Personalities
We used fairly simple prompts in our example.
But we also commented on how often the law was a social language game.
Does your analysis of a claim differ if you are an examiner versus an attorney? Or if you are a judge versus an inventor? Or a patent manager versus a CEO?
It’s an open question. My first thought is: “yes, of course it does”. Which suggests that there may be mileage in performing our analysis from different perspectives and then integrating the results. With LLMs this is often as easy as stating in the user or system prompt – “YOU ARE A PATENT EXAMINER” – this nudges the context in a particular direction. It would be interesting to see whether that makes a material difference to the mapping output.
Whole File Wrapper Analysis
In our analysis with two prior art documents, we had 10,000 tokens. These were short prior art documents and we saw there was some degradation with the longer document. But we are still only 5-10% of the available prompt context.
It is technically possible to stick in all the citations from the search report (Xs, Ys, As) and go “ANALYSE!”. Whether you’d get anything useful or trustworthy is still an open question based on the present experiments. You could also get the text from the EPO prosecution ZIP or from the US File Wrapper.
I’d imagine this is where the commercial providers will go first as it’s the easiest to implement. The work is mainly in the infrastructure of getting the PDFs, extracting the text from the PDFs, then feeding into a prompt. A team of developers at a Document Management company could build this in a week or so (I can do it in that timespan and I’m a self-taught coder). It would cost though – on my calculations around £10-15 on the API per query, so 10x+ that on charges to customers. If your query is rubbish (which is often is for the first 10 or so attempts), you’ve spent £10-15 on nothing. This is less of a no-brainer than 15p.
Looking at the results here, and from reading accounts on the web, I’d say there is a large risk of confusion in a whole file wrapper prompt, or “all the prior arts”. What happens when you have a claim 1 at the start, then 10 other claim 1s?
Most long-context models are tested using a rather hacky “needle in a haystack” metric. This involves inserting some text (often incongruous, inserted at random; machine learning engineers and proper scientists or linguistics weep now) and seeing whether the query spots it and reports accordingly. GPT4-Turbo and Claude 3 Opus seem to pass this test. But finding something is an easier task than reasoning over large text portions (it just involves configuring the attention to find it over the whole input space, which is easy-ish; “reasoning” requires attention computations over multiple separated portions).
So I predict you’ll see a lot of expensive “solutions” from those that already manage data but these may be ineffective unless you are clever. They would maybe work for simple questions, like “where is a spacer between a duct and an inner wall possibly described?” but it would be difficult to trust the output without checking or know what exactly the black box was doing. I still feel RAG offers the better solution from an explanability perspective. Maybe there is a way to lever the strengths of both?
“Harder” Technology
Actually my experience is that there is not a big drop off with perceived human difficulty of subject matter.
My experiments for hardcore A/V coding, cryptography, gene editing all show a similar performance to the mechanical example above – not perfect, but also not completely wrong. This is surprising to us, because we are used to seeing a human degradation in performance. But it turns out words are words, train yourself to spin magic in them, and one area of words is just as easy as another area of words.